Longest Common Subsequence(LCS)

Reference:

1.演算法筆記(LCS)

2.Geek面試題

3.GeeksforGeeks

DP 的精神:

遞迴分割問題時，當子問題與原問題完全相同，只有數值範圍不同，我們稱此現象為 recurrence ，再度出現、一再出現之意。

Recursive:

現在有兩個 sequence 分別為 s1 、 s2 ，現在要找出 s1 和 s2 的 LCS 。先將 s1 的最後一個元素拆出來，這個元素稱作 e1 ，而剩餘的部分稱作 sub1 好了。這裡以一道式子來簡單表示出剛剛的拆法，就是 s1 = sub1 + e1 。同樣的 s2 = sub2 + e2 。

要找出 s1 和 s2 的 LCS ，就等於是找出 sub1 + e1 和 sub2 + e2 的 LCS 。現在來觀察 sub1 、 e1 、 sub2 、 e2 與 LCS 的關係吧！首先將所有情況粗略的分做四種：

1. e1 是 LCS 的一部份，而 e2 不是；

2. e2 才是 LCS 的一部份，而 e1 不是；

3. e1 和 e2 都不是 LCS 的一部份；

4. e1 和 e2 都是 LCS 的一部份。

5. 第一種情況。如果 e1 是 LCS 的一部份，而 e2 不是，那麼對 e1 來說，在 sub2 一定要能找到一個元素，和 e1 相同，才可能形成包含了 e1 的 LCS 。以另外一個方向去思考，則可以說 e2 是沒有用的元素，要找 LCS 只需要去找 sub2 就可以了。以上可以歸納一個結論： s1 和 s2 的 LCS ，其實就是 s1 和 sub2 的 LCS ，可以把 e2 排擠掉。

6. 第二種情況。和第一種情況類似， s1 和 s2 的 LCS ，其實就是 sub1 和 s2 的 LCS 。

7. 第三種情況。如果 e1 和 e2 都不是 LCS 的一部份，那麼直接找 sub1 和 sub2 的 LCS 就好啦！

8. 第四種情況。如果 e1 和 e2 都是 LCS 的一部份，再者 e1 和 e2 都在最尾端，所以這種情況下， e1 和 e2 是一定會相等的！而且 e1 亦會是 LCS 的最後一個元素。既然 e1 、 e2 都肯定是 LCS 的最後一個元素了，那麼要找剩下的部份，只需要從 sub1 和 sub2 著手即可，如同第三種情況一般。可以歸納出一個結論： s1 和 s2 的 LCS ，必定是 sub1 和 sub2 的 LCS 在尾端加上 e1 （也是 e2 ）。

最後簡化為下面的程式:

int lcs(char *c1, int m, char *c2, int n)  
{  
    if (m == 0 || n == 0) return 0;  

    if (c1[m-1] == c2[n-1])  
    {  
        return 1 + lcs(c1, m-1, c2, n-1);  
    }  
    else  
    {  
        return max(lcs(c1, m-1, c2, n), lcs(c1, m, c2, n-1));  
    }  
}

Normal:

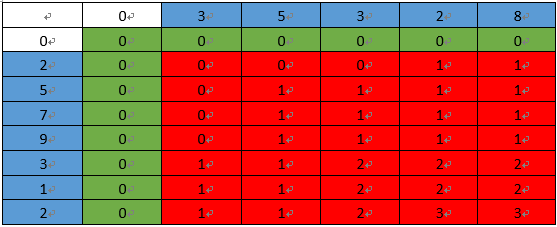
額外用到空間: 二維陣列(m*n)

int s1[7+1] = {0, 2, 5, 7, 9, 3, 1, 2};
int s2[5+1] = {0, 3, 5, 3, 2, 8};

// DP 的表格
int array[7+1][5+1];

void LCS()
{
    將 array[x][0] 和 array[0][x] 都設為 0 ;

    for (int i = 1; i <= s1_length; i++)
        for (int j = 1; j <= s2_length; j++)
            if (s1[i] == s2[j])
                // 這裡加上的 1 是指 e1 的長度為 1
                array[i][j] = array[i-1][j-1] + 1;
            else
                array[i][j] = max(array[i-1][j], array[i][j-1]);

    cout << "LCS 的長度是" << array[seq1_length][seq2_length];
}

Lower memory:

只用一維陣列(省空間),只用到n

int lcsDP3(char *c1, int m, char *c2, int n)  
{  
    vector<int> ta(n+1);  
    int t1 = 0;         //等於左上方,當字元相等時,就會用到t1
    int t2 = 0;         //就只是個暫存

    for (int i = 0; i < m; i++)  
    {  
        for (int j = 0; j < n; j++)  
        {  
            t2 = ta[j+1];  
            if (c1[i] == c2[j])  
            {  
                ta[j+1] = t1+1;  
            }  
            else  
            {  
                ta[j+1] = max(ta[j], t2);  
            }  
            t1 = t2;  
        }  
        t1 = 0;  
    }  
    return ta[n];  
}