Reverse Bits

Reference:

1. Reverse an N-bit quantity in parallel in 5 * lg(N) operations

假如給你一個正整數(32-bit)為5,二進制表示成

0000 0000 0000 0000 0000 0000 0000 0101

然後要把這二進制反轉過來變成

1010 0000 0000 0000 0000 0000 0000 0000

下面有幾種方式可以完成這功能:

Reverse_1

最直覺的方式就是一個一個去比對每個bit,當比對為1時就把1向左移動X步

每比對一次就把數字加總起來,到最後就是反轉過來的數

(X是你比對到第幾個bit)

/* Function to reverse bits of num */
unsigned int reverseBits(unsigned int num)
{
    unsigned int  NO_OF_BITS = sizeof(num) * 8;
    unsigned int reverse_num = 0, i, temp;

    for (i = 0; i < NO_OF_BITS; i++)
    {
        temp = (num & (1 << i));
        if(temp)
            reverse_num |= (1 << ((NO_OF_BITS - 1) - i));
    }

    return reverse_num;
}

Reverse_2

unsigned int ReverseBits(unsigned int n) {
    unsigned int rev = 0;

    for(int i=0; i<32; i++) 
        rev = (rev<<1) | ((n>>i) & 1); 

    return rev;
}

Reverse_3

這方式是比較特殊的,用mask的概念來對bit做操作,從下面程式碼可以看到4個mask

0x55555555, 0x33333333, 0x0F0F0F0F, 0x00FF00FF

首先讓我們來看各mask有什麼作用

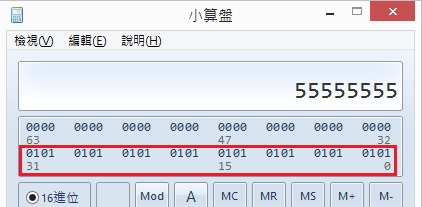
0x55555555:

可以看到二進制為0101...0101,藉由這種mask,就可以讓奇數與偶數bit的值對換,例如1010,就會變成0101

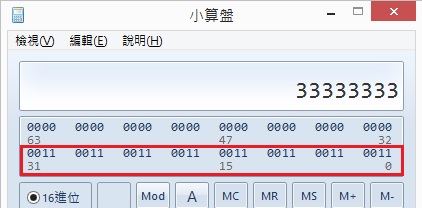
0x33333333: 可以看到二進制為0011...0011,藉由這種mask,就可以讓第一對bit與第二對bit的值做交換,例如1100,就會變成0011

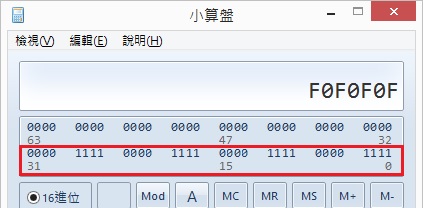
0x0f0f0f0f: 可以看到二進制為0000 1111...0000 1111,藉由這種mask,就可以讓一組四個bit與一組四個bit的值做交換,例如1001 0101,就會變成0101 1001

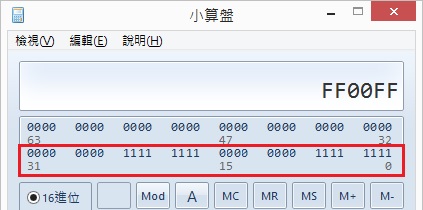
0x00ff00ff: 可以看到二進制為0000 0000 1111 1111 0000 0000 1111 1111,藉由這種mask,就可以讓一個byte與一個byte的值做交換,例如1001 0101 0000 0000,就會變成0000 0000 1001 0101

透過這樣一步一步反轉,轉到最後就把整個二進制反轉過來

unsigned int ReverseBits(unsigned int v) {
    unsigned int v; // 32-bit word to reverse bit order

    // swap odd and even bits
    v = ((v >> 1) & 0x55555555) | ((v & 0x55555555) << 1);
    // swap consecutive pairs
    v = ((v >> 2) & 0x33333333) | ((v & 0x33333333) << 2);
    // swap nibbles ... 
    v = ((v >> 4) & 0x0F0F0F0F) | ((v & 0x0F0F0F0F) << 4);
    // swap bytes
    v = ((v >> 8) & 0x00FF00FF) | ((v & 0x00FF00FF) << 8);
    // swap 2-byte long pairs
    v = ( v >> 16             ) | ( v               << 16);

    return v;
}

相關衍生問題:

有一個字串為"ab ef",如何有效率的變成"ef ab"